算法伪代码

1.1 二分检索

procedure BINSRCH(A,n,x,j)
integer low,high,mid,j,n;
low<-1; high<-n;
while low<=high do
    mid<-(low+high)/2   //取地板
    case
      :x<A(mid): high<-mid-1
      :x>A(mid): low<-mid+1
      :else: j<-mid;return;
    endcase
repeat
j<-0
end BINSRCH

1.2 二分检索改进

procedure BINSRCH1(A,n,x,j)
integer low,high,mid,j,n;
low<-1; high<-n+1
while low<high-1 do
    mid<-(low+high)/2  //取地板
    if x<A(mid)
      then high<-mid
      else low<-mid
    endif
repeat
if x=A(low) then j<-low
            else j<-0
end BINSRCH1

2.1 归并排序

Procedure MERGESORT(low,high)
int low,high,mid;
if(low<high)
    then mid<-(low+high)/2 //取地板
         call MERGESORT(low,mid)
         call MERGESORT(mid+1,high)
         call MERGE(low,mid,high)
end MERGESORT

Procedure MERGE(low,mid,high)
int h,i,j,k,low,high;
global A(low:high); local B(low:high);
h<-low;j<-mid+1;
i<-low;
while(h<=mid and j<=high) do
    if(A(h)<=A(j))then {B(i)<-A(h);h<-h+1;}
    else {B(i)<-A(j);j<-j+1;}
    i<-i+1;
repeat
if(h>mid) then for k<-j to high do {B(i)<-A(k);i<-i+1}
else for k<-h to mid do {B(i)<-A(k);i<-i+1}
for k<-low to high do A(k)<-B(k);
end MERGE

2.2 改进的归并排序

procedure MERGESORT1(low, high, p)
global  A(low:high), LINK(low:high)
if (high-low+1<16 ) then  
    call INSERTIONSORT(A, LINK, low, high, p);
else  mid<-(low+high)/2; //取地板
      call  MERGESORT1(low, mid, q);
      call  MERGESORT1(mid+1, high, r);
      call  MERGE1(q, r, p);
endif
end  MEGESORT1

procedure MERGE1(q, r, p)
global n,A(1:n),LINK(0:n);  
int  i, j, k;
i<-q;j<-r;k<-0;
while (i≠0 and j≠0) do
    if (A(i)<=A(j)) then LINK(k)<-i;k<-i;i<-LINK(i);
    else LINK(k)<-j;k<-j;j<-LINK(j);
if (i=0) then LINK(k)<-j; else LINK(k)<-i;
p<-LINK(0);
end  MERGE1

3.贪心算法-背包问题

//首先对物品按pi/wi降序排序
Procedure GREEDY-KNAPSACK(P,W,M,X,n)
real P(1:n),W(1:n),X(1:n),M,cu;
integer i,n;
X<-0;//解向量
cu<-M;//背包剩余容量
for i<-1 to n do
    if (W(i)>cu) then exit endif
    X(i)<-1
    cu<-cu-W(i)
repeat
if(i<=n) then X(i)<-cu/W(i)//放入一部分
end  GREEDY-KNAPSACK

4.贪心算法-带有期限的作业排序问题

Procedure FJS(D,n,b,J,k)
//D:作业期限，n:作业数，J:存储最优解
//b=min{ n,max{ D(i) } }
//p1>=p2>=p3...
integer b,D(n),J(n),F(0:b),P(0:b)
for i<-0 to n do
    F(i)<-i;P(i)<-1  //初值化并查集
repeat
k<-0;//初始化J
for i<-1 to n do
    j<-FIND(min(n,D(i)))  //寻找根节点
    if F(j)≠0 then J(++k)<-i;  //若还剩余可用时间片则进行分配
                   l<-FIND(F(j)-1);
                   call UNIONE(l,j);
                   F(j)<-F(l);
    endif
repeat
end FJS

5.动态规划-最优二分检索树

Procedure OBST(P,Q,n)
real P(1:n),Q(0:n),C(0:n,0:n),W(0:n,0:n),integer R(0:n,0:n),
for i<-0 to n-1 do
    (W(i,i),R(i,i),C(i,i))<-(Q(i),0,0)
    (W(i,i+1),R(i,i+1),C(i,i+1))<-(Q(i)+Q(i+1)+P(i+1),i+1,Q(i)+Q(i+1)+P(i+1)).
repeat
(W(n,n),R(n,n),C(n,n))<-(Q(n),0,0)

for m<-2 to n do
  for i<-0 to n-m do
    j<-i+m
    W(i,j)<-W(i,j-1)+P(j)+Q(j)
    k<-区间[R(i,j-1),R(i+1,j)]中使{C(i,l-1)+C(l,j)}取最小值的l值
    C(i,j)<-C(i,k-1)+C(k,j)+W(i,j)
    R(i,j)<-k //记录a_k为树根
  repeat
repeat
end OBST

6.动态规划-矩阵链乘积问题

Procedure Matrix-Chain-Order(n)
int m(1:n,1:n),s(1:n-1,1:n)//m:乘法次数，s:记录分割点
for i=1 to n-1 do
  (m(i,i),s(i,i))<-(0,0)
  (m(i,i+1),s(i,i+1))<-(p_i-1 p_i p_i+1,i)
repeat
(m(n,n),s(n,n))<-(0,0)
for w<-2 to n-1 dp
  for i<-1 to n-w do
    j<-i+w
    k<-区间[i,j)中使{m(i,l)+m(l+1,j)+p_i-1 pl pj}取最小值的l
    m(i,j)<-m(i,k)+m(k+1,j)+p_i-1 pk pj
    s(i,j)<-k
  repeat
repeat

7.动态规划-最长公共子序列问题

Procedure LCS-Length(X,Y)
m=X.length;n=Y.length//长度矩阵：C[m,n],标记矩阵:B[m,n]
For i=1 to m
  C[i,0]=0
For j=1 to n
  C[0,j]=0
For i=1 to m
  For j=1 to n
    if X[i]==Y[j] then C[i,j]=C[i-1,j-1]+1;B[i,j]="↖"
    else if C[i-1,j]>=C[i,j-1] then C[i,j]=C[i-1,j];B[i,j]="↑"
    else C[i,j]=C[i,j-1];B[i,j]="←"
return C and B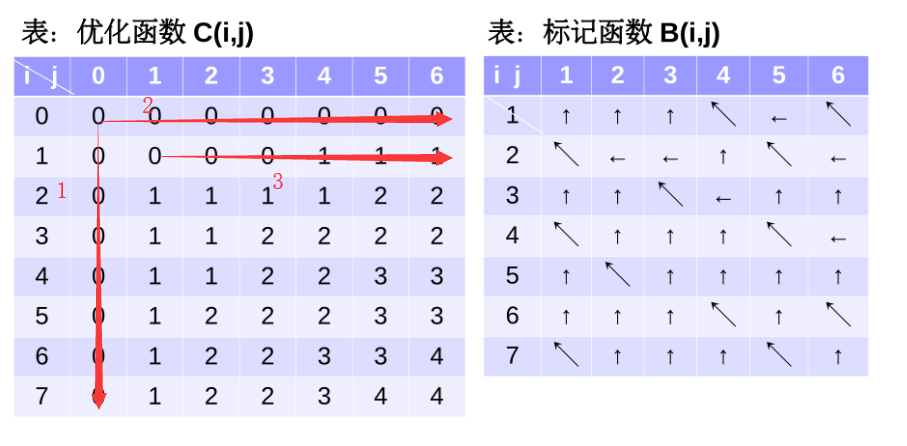

8.回溯法-八皇后问题

Procedure PLACE(k)
int i,k;
i<-1;
while(i<k) do//依次判断是否与1到k-1的皇后发生冲突
  if(X(i)=X(k) or ABS(X(i)-X(k))=ABS(i-k)) then
    return false;
  endif
  i<-i+1;
repeat
return true;
end PLACE

Procedure NQUEENS(n)
int k,n,X(1:n);
k<-1;X(1)<-0;
while(k>0) do
  X(k)<-X(k)+1; //移到下一列
  while(X(k)<=n and Not PLACE(k)) do //X(k)位置发生冲突，则尝试下一列
    X(k)<-X(k)+1;
  repeat
  if(X(k)<=n) then
    if(k=n) then  //说明已得到一解
      print(X);
    else {k<-k+1;X(k)<-0;} //处理下一个皇后
    endif
  else k<-k-1;  //说明当前走法无解，则回溯
  endif
repeat
end NQUEENS

9.回溯法-子集合数问题

Procedure SUMOFSUB(s,k,r)
global integer M,n;global integer W(1:n);global boolean X(1:n)
integer r,s;integer k
//W(j)为各权值，按升序排序；X(j)为解向量元素，取1或0
//在进入此过程时X(1)...X(k-1)的值已经确定
X(k)<-1
if s+W(k)=M
  then print(X)
else
  if s+W(k)+W(k+1)<=M
    then call SUMBOFSUB(s+W(k),k+1,r-W(k))//递归入口,表示已选择此元素
  endif
endif
if s+r-W(k)>=M and s+W(k+1)<=M
  then X(k)<-0
    call SUMOFSUB(s,k+1,r-W(k))//递归入口，表示不选择此元素
endif
end SUMOFSUB

10.LC检索一般方法

Procedure LC(T,c)
E<-T
置活节点表为空
loop
  if E是答案节点 then 输出从E到T的路径 return endif
  for E的每一个儿子X do
    call ADD(X); PARENT(X)<-E
  repeat
  if 不再有活节点 then print('No answer')
    stop
  endif
  call LEAST(E)//从活节点表内选择c最小的
repeat
End LC